Теперь рассмотрим, как можно использовать уравнения движения по координатным осям для решения задачи динамики движения одного тела (материальной точки), на которое действуют несколько сил. Отметим, что все задачи динамики движения материальной точки решаются по одинаковой схеме.
Дано: По плоскости, образующей с горизонтом угол а, соскальзывает вниз брусок массой m. Найдите ускорение бруска, если известно, что коэффициент трения бруска о плоскость равен µ.
Решение.
Шаг 0. Будем считать брусок материальной точкой.
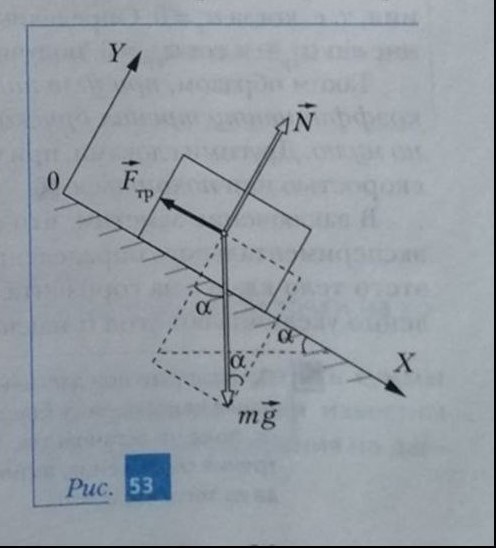
Шаг 1. Выберем в качестве тела отсчета наклонную плоскость. Оси Х и Y направим так, как показано на рис. 53.
Шаг 2. Изобразим действующие на брусок силы: силу тяжести mg, силу реакции опоры N и силу трения скольжения Fтр
Шаг 3. Определим проекции сил на координатные оси.
Начнем с оси Х. Проекция силы реакции опоры N равна нулю, так как она перпендикулярна оси Х. Проекция силы тяжести положительна и равна mg = mg sin a. Проекция силы трения отрицательна и равна Fтрx=-Fтр. Таким образом, сумма проекций на ось Х всех действующих на брусок сил равна mg sin a — Fтр. Теперь определим проекции сил на ось Ү. Проекция силы реакции опоры N положительна, поэтому Ny = N. Проекция силы трения равна нулю, так как она перпендикулярна оси Y. Проекция силы тяжести mg отрицательна и равнa mgx = -mg cos а. Следовательно, сумма проекций сил на ось Y равна N — mg cos a.
Шаг 4. Запишем второй закон Ньютона в проекциях на координатные оси:
N-mg cos a = may
mg sin a — Fтр=max
Шаг 5. По условию задачи брусок скользит вниз по наклонной плоскости. Следовательно, сила трения Fтр, является силой трения скольжения. Поэтому Fтр = µN.
Шаг 6. По условию задачи в выбранной нами системе отсчета брусок движется только вдоль оси Х. Поэтому аy = 0.
Шаг 7. Система уравнений имеет вид:
(1) N — mg cos a = may
(2) mg sin a — Fтр=max
(3) Fтр = µN,
(4) ax=0.
Шаг 8. Решая уравнения, подставим уравнение (4) в уравнение (1). Получим: N = mg cos а. Подставляя найденное выражение для N в уравнение (3). получаем: Fтр = µN = µmg cos a.
Подставляя Fтр в уравнение (2), имеем: mg sin a — µmg cos a = max
Следовательно, после деления обеих частей уравнения на m: ax = g (sina — μ cos α).
Шаг 9. Проведем анализ полученного результата. Из ответа следует, что с увеличением угла, а его синус будет возрастать до 1, а его косинус уменьшаться до нуля. Поэтому с увеличением, а модуль аx ускорения также будет увеличиваться. Если а достигнет 90°, то ускорение будет равно: Ax = g(sin 90° — µ cos 90°) = g. Другими словами, при угле наклона 90° брусок перестанет взаимодействовать с плоскостью (N = 0, Fтр = 0) и его движение будет свободным падением. Полученное выражение позволяет также найти значение угла а, при котором брусок будет находиться в состоянии покоя или равномерного движения, т. е. когда аx = 0. Определим этот угол, обозначив его aкр. Решив уравнение sin aкр — µ cos aкр = 0, получим: tg aкр = μ.
Таким образом, при угле наклона плоскости, тангенс которого равен коэффициенту трения бруска об эту плоскость, ускорение бруска равно нулю. Другими словами, при угле aкр брусок будет двигаться с постоянной скоростью или покоиться.

